engineering notes: Engineering mechanics

Thursday, August 5, 2010

1.free body diagram discription

Free body diagram

A free body diagram is a pictorial representation often used by physicists and engineers to analyze the forces acting on a body of interest. A free body diagram shows all forces of all types acting on this body. Drawing such a diagram can aid in solving for the unknown forces or the equations of motion of the body. Creating a free body diagram can make it easier to understand the forces, and torques or moments, in relation to one another and suggest the proper concepts to apply in order to find the solution to a problem. The diagrams are also used as a conceptual device to help identify the internal forces—for example, shear forces and bending moments in beams—which are developed within structures.^[1]^[2]

1 Construction
- 1.1 What is included
- 1.2 What is excluded
- 1.3 Assumptions
2 Example
3 See also
4 References

Construction

A free body diagram consists primarily of a sketch of the body in question and arrows representing the forces applied to it. The selection of the body to sketch may be the first important decision in the problem solving process. For example, to find the forces on the pivot joint of a simple pair of pliers, it is helpful to draw a free body diagram of just one of the two pieces, not the entire system, replacing the second half with the forces it would apply to the first half.

What is included

The sketch of the free body need include only as much detail as necessary. Often a simple outline is sufficient. Depending on the analysis to be performed and the model being employed, just a single point may be the most appropriate. If rotation of the body and torque is in consideration, it is best to draw the shape. Free body diagrams are named as such because the diagram isolates the body, hence free, from all other interacting bodies, and the diagram focuses on one specific body. Neighboring free body diagrams in the same big picture may be necessary in order to consider the other interacting bodies of the situation.
All external contacts, constraints, and body forces are indicated by vector arrows labeled with appropriate descriptions. The arrows show the direction and magnitude of the various forces. To the extent possible or practical, the arrows should indicate the point of application of the force they represent.
Only the forces acting on the object are included. These may include forces such as friction, gravity, normal force, drag, tension, normal force, or a human force due to pushing or pulling. When in a non-inertial reference frame, fictitious forces, such as centrifugal pseudoforce may be appropriate.
A coordinate system is usually included, according to convenience. This may make defining the vectors simpler when writing the equations of motion. The x direction might be chosen to point down the ramp in an inclined plane problem, for example. In that case the friction force only has an x component, and the normal force only has a y component. The force of gravity will still have components in both the x and y direction: mgsin(θ) in the x and mgcos(θ) in the y, where θ is the angle between the ramp and the horizontal.

What is excluded

All external contacts and constraints are left out and replaced with force arrows as described above.
Forces which the free body applies to other objects are not included. For example, if a ball rests on a table, the ball applies a force to the table, and the table applies an equal and opposite force to the ball. The FBD of the ball only includes the force that the table causes on the ball.
Internal forces, forces between various parts that make up the system that is being treated as a single body, are omitted. For example, if an entire truss is being analyzed to find the reaction forces at the supports, the forces between the individual truss members are not included.
Any velocity or acceleration is left out. These may be indicated instead on a companion diagram, called "Kinetic diagrams", "Inertial response diagrams", or the equivalent, depending on the author.

Assumptions

The free body diagram reflects the assumption and simplifications made in order to analyze the system. If the body in question is a satellite in orbit for example, and all that is required is to find its velocity, then a single point may be the best representation. On the other hand, the brake dive of a motorcycle cannot be found from a single point, and a sketch with finite dimensions is required.
Force vectors must be carefully located and labeled to avoid assumptions that presuppose a result. For example, in the accompanying diagram of a block on a ramp, the exact location of the resulting normal force of the ramp on the block can only be found after analyzing the motion or by assuming equilibrium.
Other simplifying assumptions that may be considered include two-force members and three-force members.

Example

A simple free body diagram, shown above, of a block on a ramp illustrates this.

All external supports and structures have been replaced by the forces they generate. These include:

mg: the product of the mass of the block and the constant of gravitation acceleration: its weight.
N: the normal force of the ramp.
F_f: the friction force of the ramp.

free body diagram for friction

The force vectors show direction and point of application and are labeled with their magnitude.
It contains a coordinate system that can be used when describing the vectors.

E.Mech-1.Introduction

Introduction

The goal of this Engineering Mechanics course is to expose students to problems in mechanics as applied to plausibly real-world scenarios. Problems of particular types are explored in detail in the hopes that students will gain an inductive understanding of the underlying principles at work; students should then be able to recognize problems of this sort in real-world situations and respond accordingly.

Further, this text aims to support the learning of Engineering Mechanics with theoretical material, general key techniques, and a sufficient number of solved sample problems to satisfy the first objective as outlined above.

Distinction between branches of physics

Most applied branches of classic physics in engineering

As you see in the diagram mechanics is the first and most fundamental branch of physics, supporting Thermodynamics and Electricity, and including Statics, Dynamics(=Kinematics+kinetics); all which are all highly applicable in engineering. but the most important part of them is statics (study of body at rest) which is not only a base for all others, but also have the highest engineering application. physics also involve optics, waves, quantum, and relativity theory, which have no fundamental engineering application yet.

Distinction between classic and modern physics

Distinction between Physics and Engineering physics

Difference of pure and applied science

Distinction between branches of Engineering mechanics

Prerequisites

This book assumes familiarity with high school physics and calculus, although the mathematics used is fairly elementary.

Statics

We describe the motion of bodies using Newton's second law of motion

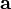$\text{Force = Mass * Acceleration} \qquad \text{or} \qquad \mathbf{f} = m~\mathbf{a} \,$

Statics deals with the situation where the acceleration ( $\mathbf{a}\,$ ) is zero - which happens when a body is at rest, or moving with constant velocity. That means that the total force on a body at rest or with constant velocity must be zero. In other words, the sum of the forces on the body must equal zero.

$\text{Sum of Forces = 0} \qquad \text{or} \qquad \sum \mathbf{f} = \mathbf{0}$

Engineers typically draw what is called a "free body diagram" to show all forces on a body at rest. These forces are then broken down into vectors consistent with a useful coordinate system and summed in sets (components parallel to each basis vector) which are then set to zero to meet the static constraint of no acceleration being present.
This typically results in sets of equations which can be solved using simple linear algebra techniques or even simple algebra and substitution.

Truss

Forces act along the members, and there are no shear forces or moments. A truss is therefore defined as a system composed entirely of two-force members, which only carry axial loads. The ends of a truss are pinned, so that they don't carry moments. The only reactions at the ends of a truss member are forces. External forces on trusses act only on the end points. Truss problems are solved by the method of sections, where an imaginary cut is made through the member(s) of interest, and global equilibrium of forces and moments are used to determine the forces in the members, or by the method of joints, in which a single joint is isolated and analyzed and the resulting forces (not necessarily with a numerical value) are transferred to adjacent joints, where the process is repeated. The resulting set of equations can then be solved by linear algebra, or substitution.

Chains and Cables

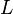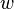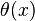Chains and cables are attached at end points and have a continuous load on them due to their own weight (body forces) or external loads. Let a cable of length $L\,$ have a load of $w\,$ acting per unit distance between the supports. If the tension in the cable at any point is $T(x)\,$ , then we have, for an infinitesimal length of the cable making an angle $\theta(x)\,$ with the horizontal,

$\begin{align} \cfrac{d}{dx}[T~\cos\theta] = 0 \\ \cfrac{d}{dx}[T~\sin\theta] = w \end{align}$

Thus, we have,

$\begin{align} T~\cos\theta = \text{constant} = K \\ T~\sin\theta = \int w~dx + C_1 \end{align}$

$\tan\theta = \cfrac{1}{K}~\left[\int w~dx + C_1 \right]$

Now

$\tan\theta = \cfrac{dy}{dx} ~.$

So we have a differential equation for $y\,$ in terms of $x\,$ :

$\cfrac{dy}{dx} = \cfrac{1}{K}~\left[\int w~dx + C_1 \right]$

Solving for $y\,$ ,

$y = \cfrac{1}{K}~\left[\int \left(\int w~dx\right)~dx + C_1~x + C_2 \right]$

If $w\,$ is a constant, then we have,

$y = \cfrac{1}{K}~\left[\cfrac{w~x^2}{2} + C_1~x + C_2 \right]$

which is the equation of a parabola.
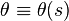For a rope where the loading is given in terms of the length of the rope (much more common), i.e., $T \equiv T(s)$ and $\theta \equiv \theta(s)$ , we have,

$\begin{align} \cfrac{d}{ds}[T~\cos\theta] & = 0 \\ \cfrac{d}{ds}[T~\sin\theta] & = w(s) \end{align}$

where

$ds = \sqrt{dx^2 + dy^2}$

Dynamics

While statics deal with the part of mechanics where all objects are stationary, dynamics deals with objects or structures with a non-zero acceleration. Dynamics may be broken down into kinematics and kinetics. Kinematics deal with displacement, velocities and accelerations without concern for the forces involved. Kinetics deal with the forces and moments involved in making the body move.